FREE 10+ Proportional Relationship Samples in PDF | DOC

We all know that water is vital in keeping our health to its optimal state. It eliminates the waste from our body through urination, perspiration, and bowel movement. It also allows your body to maintain a normal temperature and protect body tissues. However, you should also know that there is a specific amount of water that one person should take to maintain one’s health. For men, the amount of water that one should take in a day is about 3.7 liters. Meaning, in a week, a man should take 25.9 liters of water. It is just an example of a Proportional Relationship, which in real life, just like a personal budget, we use more often than you think.

What is a Proportional Relationship

Simply put, you can say that the two variables have a Proportional Relationship if their ratios are equal. You can use this mathematical method to express the two variables that vary from the other. For example, 1/2 has a proportional relationship with 2/4. Needless to say, they are equal. Refer to the situation that we mentioned earlier. In a day, a man needs to drink 3.7 liters, making it 25.9 liters in 7 days. To make it simpler, we can express it in the form of a ratio. One is to 3.7(1:3.7) has a directly proportional relationship to 7:25.9.

Types of Proportional Relationship

In determining if a proportional relationship exists in the set of variables, you should specify what type of proportional relationship you are looking for, which we are going to discuss in this section.

1. Directly Proportional Relationship

You can say if a set of variables is directly proportional if one variable increases if the other variable rises at the same rate. For example, the amount you earn in working a company is directly proportional to the number of hours that you work. Another example is if 10-meter rope weighs 1/2 kilo, and a 20-meter rope weighs 1 kilo, then the two variables are directly proportional. How? As you can see, the length and the weight of both ropes are directly proportional. If you multiply 10 meters to 2, the result is 20 meters. If you do the same to its weight, the result is 1 kilo, making it proportional. Meanwhile, since it appears that the value of the second variable is increasing in proportion to the first one, we can refer to it as directly proportional.

2. Inversely Proportional Relationship

In contrast to the directly proportional relationships, you can determine that a set of variables has an inversely proportional relationship if the value of a variable decreases while the other is increases. For example, speed and travel time have an inversely proportional relationship because as your speed increases while running, the shorter the time you need to cover a particular area.

10+ Proportional Relationship Samples

Did you know that, according to Perkins E-learning, students learn Proportional relationships during their 6th grade and 7th grade? However, it does not mean that you can’t relearn it if you are already in the 8th grade or any other level. As we have mentioned earlier, you can use this type of math method in the real world. Thus, there is no reason not to reacquire this learning even if you have graduated from grade school. In this section, we have gathered samples and templates, which you can use if you want to expand your knowledge about Proportional Relationship.

1. Proportional Relationship Sample

2. Basic Proportional Relationship Template

3. Identifying and Representing Proportional Relationships Sample

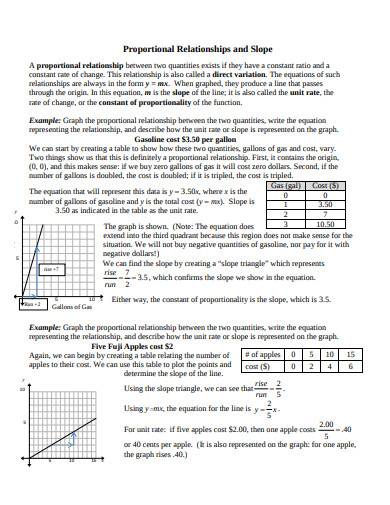
4. Proportional Relationship and Slope Template

5. Standard Proportional Relationship Sample

6. Proportional Relationship Worksheet Template

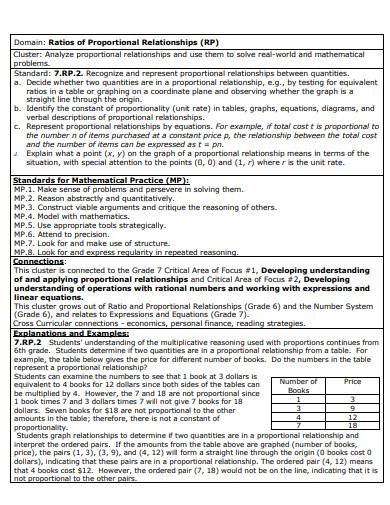
7. Ratios of Proportional Relationship Template

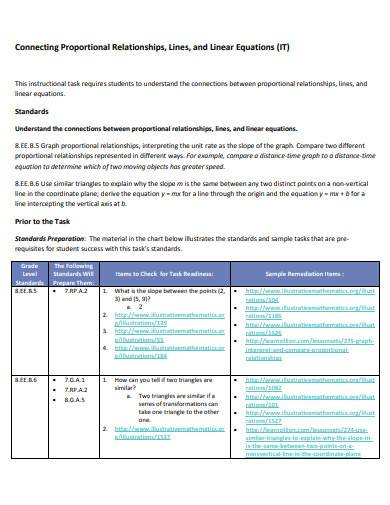
8. Connecting Proportional Relationship Template

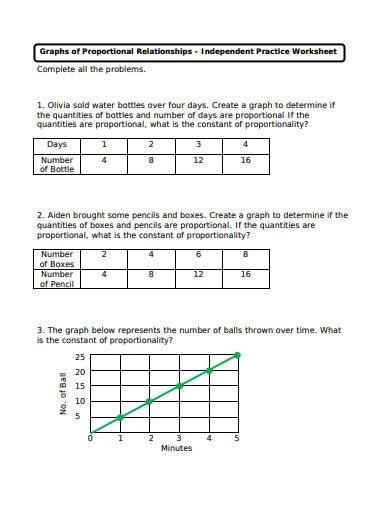
9. Graphs of Proportional Relationship Sample

10. Proportional and Linear Relationship in DOC

11. Proportional Relationship in DOC

 

How to Determine if Proportional Relationships Exist

There are a few ways to determine if a proportional relationship exists, which we are going to discuss in this section.

1. Fractions

You can say that a set of fractions has a proportional relationship if both of them result in the same value after reduction. Take {2/14, 1/7} as an example. If you divide 2/14 to 2/2, the result is 1/7. Meanwhile, no need to reduce the second number since it is already in a reduced value.

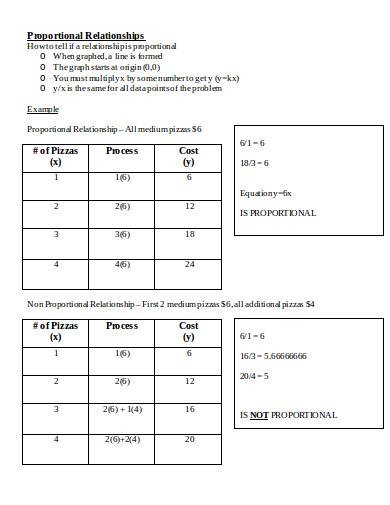
2. Table

It is somehow similar to the fractions. However, in this method, you are using a table. It also intends to solve a different problem. With the use of ratios, you can determine if the chart shows a proportional relationship. Take note, though, that not all data within a table are proportional. Thus, it is crucial to check all the information to determine if a proportional relationship exists.

3. Coordinate Graph

Same with the table, not all coordinates in a graph indicates a proportional relationship. You can say if the coordinates have a proportional relationship if both of them lie within a straight line from the origin. It happens when x and y coordinates.

Proportional Relationships for the Students with Visual Impairments

Now you know what a Proportional Relationship is and how to determine if the given variables are proportional or non-proportional. However, has it ever cross your mind how the blind students tackle this type of lesson? Do they encounter any challenges? How can they overcome these difficulties?

Recognizing and representing proportional relationships is one of the most difficult challenges they face. If you are teaching students with visual impairments, you can mitigate this problem by using braille or large print ruler and sliders, tactile fractional circles, and graphics on a coordinate plane, timer, Math builder, graph board, embossed graph sheets, and manipulatives.

Learning about Proportional Relationships is indeed vital in our daily lives, may it be at home or the office. In this article, we have discussed the things that you need to know about proportional relationships. However, you should also know that this mathematical method is just one of the many that you can learn and use in your daily life. Start by reading our article about personal financial statements.