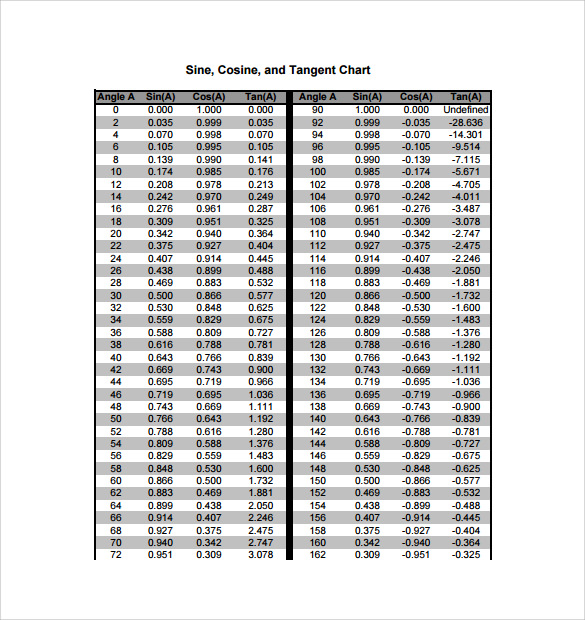
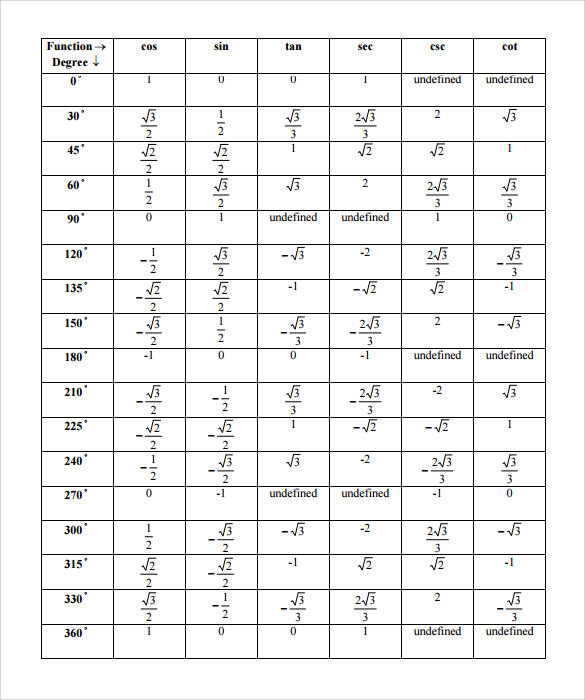
Sin Cos Tan Chart is very important for higher mathematics students and teachers alike. This chart is also called trigonometric chart which contains the trigonometric angular values of sin, cos, tan, cot, sec and cosec from the angle 00 to 900. Students and teachers use this readymade chart to refer to any angular value of these trigonometric functions. You may also see unit circle charts.
There is also a specific way to remember the values of these trigonometric functions without cramming blindly. As a whole, Sin Cos Tan chart is a must keep for every mathematics students, which after a few days they could easily remember without referencing them. You may also see math charts.
Sin Cos Tan Chart Template
Sample Sine Cosine Tangent Chart Degrees Template
How to Find Sin Cos Tan Values?
Finding the values of sine (sin), cosine (cos), and tangent (tan) for specific angles is a fundamental aspect of trigonometry, a branch of mathematics. These functions relate the angles of a triangle to the lengths of its sides and have important applications in various fields such as physics, engineering, and computer science. Here’s how you can find these values:
For Standard Angles
The sine, cosine, and tangent values for standard angles (like 0°, 30°, 45°, 60°, and 90°) can often be memorized using specific trigonometric identities or ratios derived from geometric considerations. For these angles, the values are typically:
- 0°: sin(0°) = 0, cos(0°) = 1, tan(0°) = 0
- 30°: sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
- 45°: sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1
- 60°: sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3
- 90°: sin(90°) = 1, cos(90°) = 0, tan(90°) = Undefined
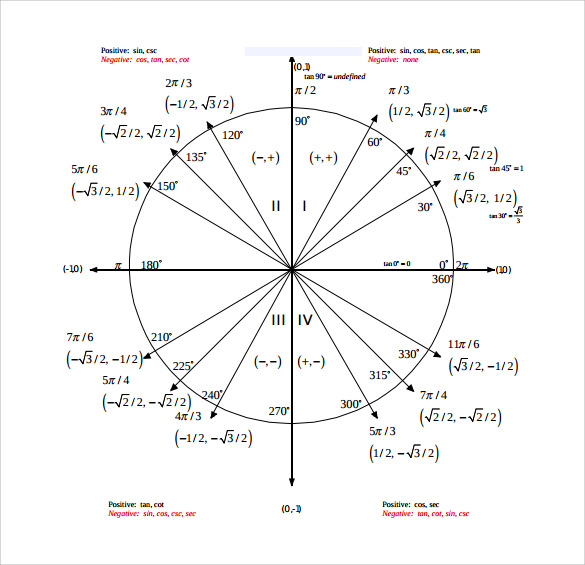
Using the Unit Circle
The unit circle is a circle of radius 1 centered at the origin of a coordinate plane. It can be used to find the sine and cosine values of any angle, measured from the positive x-axis. In this context:
- Sine of an angle is the y-coordinate of the point where the angle’s terminal side intersects the unit circle.
- Cosine of an angle is the x-coordinate of that point.
- Tangent can be found by dividing the sine of the angle by its cosine (tan = sin/cos).
Calculators and Software
For non-standard angles or when precision is needed, sine, cosine, and tangent values can be found using scientific calculators or software programs that have trigonometric function capabilities. You simply input the angle (in degrees or radians) into the function you need (sin, cos, or tan) to get the value.
Mathematical Series
For angles not easily derived from the unit circle or standard values, the sine, cosine, and tangent values can also be calculated using infinite series such as the Taylor or Maclaurin series. However, this method is more complex and typically used for theoretical purposes or within software implementations.
Conversion Between Degrees and Radians
When using trigonometric functions, it’s important to know if your calculator or software expects the angle in degrees or radians. To convert:
- From degrees to radians: multiply by π/180.
- From radians to degrees: multiply by 180/π.
Understanding how to find these values, and being able to use them appropriately, is crucial for solving problems in trigonometry and applying these concepts in practical scenarios.
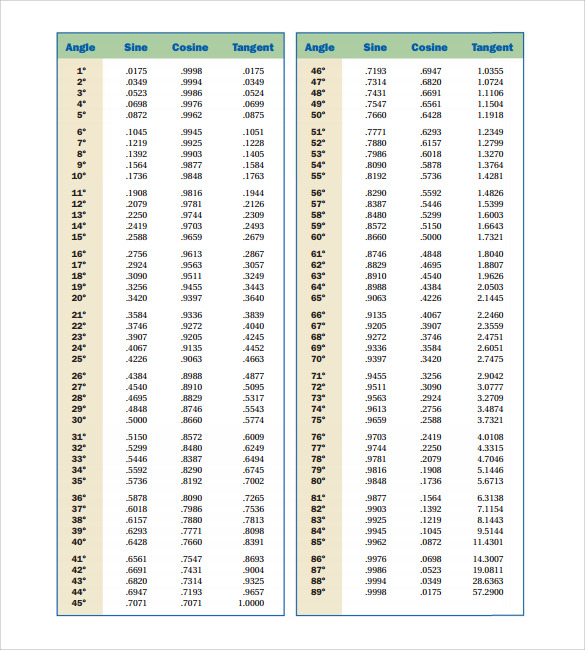
Sin Cos Tan Chart Template
Values Of Sin Cos Tan Chart Template
Tips to Remember Sin Cos Tan Chart
Remembering the sine (sin), cosine (cos), and tangent (tan) values for common angles can be challenging at first, but there are several tips and tricks that can help you memorize them more easily. Here are some strategies:
1. Special Triangles
Understanding the geometry of the special right-angled triangles can greatly help:
- 45°-45°-90° Triangle: In this isosceles right triangle, the sides opposite the 45° angles are equal, and the hypotenuse is √2 times longer than each leg. Therefore, sin(45°) = cos(45°) = 1/√2, and tan(45°) = 1.
- 30°-60°-90° Triangle: This triangle can be formed by cutting an equilateral triangle in half. The side opposite the 30° angle is half the hypotenuse, and the side opposite the 60° angle is √3 times the shorter leg. This gives sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3, and so forth for the 60° angle.
2. Mnemonics
Create a mnemonic to remember the basic values. For example, for the sine values of the angles 0°, 30°, 45°, 60°, and 90°, remember the sequence 0, 1/2, √2/2, √3/2, 1. A common mnemonic is:
- “Old Harry And His Old Aunt” — stands for 0, 1/2 (√1/2), √2/2, √3/2, 1. Each phrase’s initials represent the sequence of sine values (you can use a similar approach for cos and tan).
3. The Unit Circle
Familiarize yourself with the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate system. Knowing the positions of the standard angles on the unit circle can help you visualize and remember their sine and cosine values:
- The x-coordinate of a point on the unit circle corresponds to the cosine of the angle.
- The y-coordinate corresponds to the sine of the angle.
4. Sine, Cosine, and Tangent Functions
Understand the relationship between the sine, cosine, and tangent functions:
- Tangent is the ratio of sine to cosine (tan = sin/cos).
- The cosine of an angle is the sine of its complement (cos(θ) = sin(90°-θ)).
- Remembering the values for sine can help you derive the values for cosine and vice versa.
5. Practice and Repetition
The more you work with these values and use them in problems, the more familiar they will become. Practice by solving a variety of trigonometry problems.
6. Visual Aids
Create or find sample charts and diagrams that display the values of sine, cosine, and tangent for the standard angles. Having a visual reference can aid in memorization.
7. Use Technology
There are various educational apps and online resources that offer interactive ways to learn and remember trigonometric values. These can provide additional practice and reinforcement.
Combining these strategies can make it easier to remember the sine, cosine, and tangent values for the key angles in trigonometry, aiding both in academic studies and in practical applications.
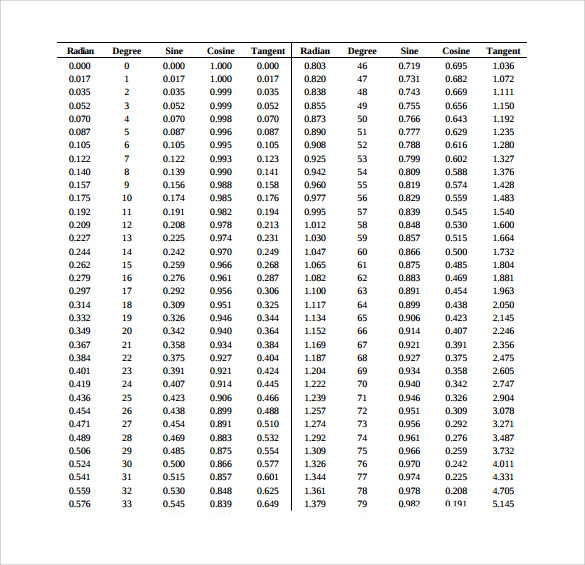
Basic Sin Cos Tan Chart Template
Unit Circle Sin Cos Tan Chart Template
Trick to Remember the Formula to Find Sin Cos Tan Chart
A popular and effective trick to remember the sine (sin), cosine (cos), and tangent (tan) values for the most common angles (0°, 30°, 45°, 60°, and 90°) involves using your hands. This method provides a quick and visual way to recall the values without needing a chart. Here’s how it works:
Hand Trick for Sin, Cos, and Tan Values
- Assign Fingers to Angles:
- Extend your left hand with your palm facing you.
- Assign each finger to an angle, starting from your thumb to your little finger as 0°, 30°, 45°, 60°, and 90° respectively.
- Finding Sine Values:
- For sine values, touch the tip of the thumb or any finger representing the angle you’re interested in with your other hand.
- Count the number of fingers including and to the left of the touched finger. This count represents the numerator.
- The denominator is always 2 raised to the power of 2 (or simply 4).
- The value is then the square root of the numerator divided by the denominator. For example, for sin(30°), touch your index finger and count 1 finger to the left of it (including the index finger). So, sin(30°) = √1/2, but since we typically rationalize it, it becomes 1/2.
- Finding Cosine Values:
- Cosine values follow the same procedure but in reverse order. Touch the finger for the angle you’re interested in, but this time, count the fingers to the right (including the touched one).
- For example, for cos(30°), touch your index finger and count 4 fingers to the right (including the index finger). So, cos(30°) = √4/2 = √(4/4) = 1/√2, which simplifies to √3/2.
- Tangent Values:
- Since tangent is the ratio of sine to cosine (tan(θ) = sin(θ)/cos(θ)), you can find the tangent values by dividing the sine value by the cosine value for any given angle.
- Alternatively, remembering the basic tan values for these angles or understanding the pattern can help, as tan values are not as straightforwardly visualized with this hand method.
Example:
- To Find sin(60°) and cos(60°):
- For sin(60°), touch your ring finger and count 3 fingers to the left of it (including the ring finger). Sin(60°) = √3/2.
- For cos(60°), touch your ring finger and count 2 fingers to the right of it (including the ring finger). Cos(60°) = √1/2, which is simplified to 1/2.
Advantages of the Hand Trick:
- It’s a quick and easy way to recall the trigonometric values for common angles without having to memorize a chart.
- It visualizes the concept, making it easier to remember.
- It’s particularly useful for quick calculations and checks during exams or while studying.
While this trick covers the basic angles, understanding how these values are derived and being able to visualize them on the unit circle can further deepen your comprehension of trigonometry.
Unit Circle Sin Cos Tan Positive Chart Template
How to calculate sine?
To calculate sine for an angle in a right triangle, divide the length of the side opposite the angle by the length of the hypotenuse.
What are sin cos and tan short for?
“Sin” stands for sine, measuring the ratio of the opposite side to the hypotenuse. “Cos” is cosine, the adjacent side to hypotenuse ratio. “Tan” is tangent, the opposite over adjacent.
What is the basic sine rule?
The basic sine rule states that in any triangle, the ratio of a side length to the sine of its opposite angle is constant.
What is the value of sin 0°?
The value of sin 0° is 0. This is because the opposite side of a 0° angle in a right triangle has zero length.
How do I know if I should use sin cos or tan?
Use sin when you have or need the opposite side and hypotenuse, cos for the adjacent side and hypotenuse, and tan for the opposite and adjacent sides.
What is the sine and cosine rule?
The sine rule relates sides and angles in any triangle: a/sin(A) = b/sin(B) = c/sin(C). The cosine rule relates the lengths of a triangle’s sides to one of its angles: c^2 = a^2 + b^2 – 2ab*cos(C).
In conclusion, the sine, cosine, and tangent chart serves as a valuable tool for understanding trigonometric functions and solving mathematical problems involving angles and triangles. With its systematic layout and clear values, it aids in mathematical analysis and problem-solving.
If you have any DMCA issues on this post, please contact us!
Related Posts
Self Introduction Speech Examples
Business Profile Samples
Biography Samples
Sample Research Reports
Salutatorian Speech Samples
Sample Key Log Templates
Sample User Manual Templates
Sample Graduation Speech
Rental Ledger Templates
Sample Delivery Note Templates
Sample Discursive Writing Templates
Sample Handover Reports
Research Paper Examples
Research Paper Samples
Sample Payment Vouchers Templates